Deep Learning - ANN - Artificial Neural Network - Weight Initialization Techniques Tutorial
How to Initialize Weight?
1] Initialize the parameters
2] Choose an optimization algorithm
3] Repeat these steps:
- Forward propagate an input
- Compute the cost function
- Compute the gradients of the cost with respect to parameters using backpropagation.
- Update each parameter using the gradients, according to the optimization algorithm
The problem occurs if the incorrect weight initialized is-
1] Vanishing Gradient Problem
2] Exploding Gradient Problem
3] Slow Convergence
What not to do?
1] Not to initialize weight with zero
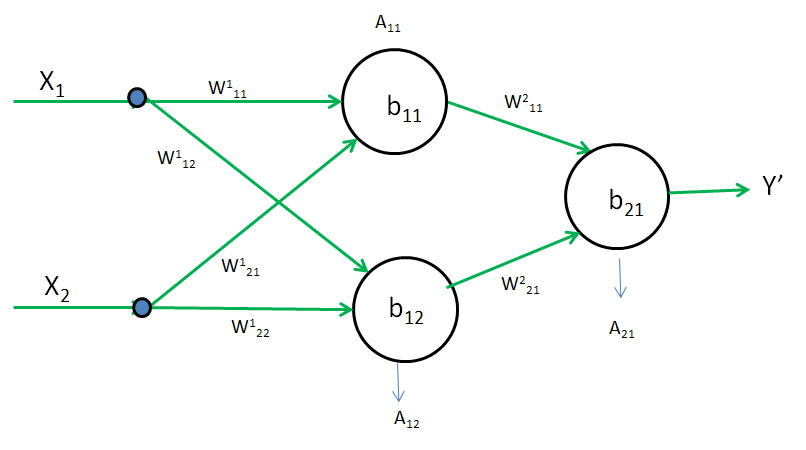
Case 1] Lets Take A11 and A12 as a Relu Activation Function
A11 = max(0, Z11)
Z11 = W111X1 + W121X2 + b11
A12 = max(0, Z12)
Z12 = W112X1 + W122X2 + b12
Now assume W=0, b=0. therefore Z11 = 0 and Z12 = 0. Due to this A11 and A12 both will become zero.
As A11 and A12 are zero due to which \(\frac{\delta L}{\delta W^1_{11}}\) is also becomes zero.
W111(new) = W111(old) - \(\eta\frac{\delta L}{\delta W^1_{11}}\)
Therefore,W111(new) = W111(old) and No training will take place
Zero Initialization Relu Practical
Case 2] Lets Take A11 and A12 as a Tanh Activation Function
A11 = \(\frac{e^{Z_{11}} - e^{-Z_{11}}}{e^{Z_{11}} + e^{-Z_{11}}}\)
As Z11 = 0. Due to this A11 will become zero. Similarly, A22 will also become zero
As A11 is zero due to which \(\frac{\delta L}{\delta W^1_{11}}\) is also becomes zero.
W111(new) = W111(old) - \(\eta\frac{\delta L}{\delta W^1_{11}}\)
Therefore,W111(new) = W111(old) and No training will take place
Case 3] Lets Take A11 and A12 as a Sigmoid Activation Function
A11 = \(\sigma(Z_{11}) =0.5\)
On Zero Sigmoid value is 0.5. Similarly, A22 will also become 0.5
In this, weights W111 and W112 will act as a single weight and W121 and W122 will act as a single weight and both single weights will go into one neuron. In short, if there is 1000 neuron then all 1000 neuron act as a single neuron
Therefore, it will not be able to capture non-linearity and it will act or behave like a perceptron
W111(new) = W111(old) - \(\eta\frac{\delta L}{\delta W^1_{11}}\)
Therefore,W111(new) = W111(old) and No training will take place
Zero Initialization Sigmoid Practical
2] Not to initialize weight with a constant non-zero value
Let's assume all weight and bias are non-zero constants i.e. 0.5.
A11 = max(0, Z11) → Non-Zero
Z11 = W111X1 + W121X2 + b11 → Non-Zero
A12 = max(0, Z12) → Non-Zero
Z12 = W112X1 + W122X2 + b12 → Non-Zero
therefore, Z11 = Z12 and A11 = A12
In this, if you put multiple neurons in the single hidden layer, it will act as a single neuron and is not able to capture non-linearity. The model will remain linear.
3] Not to initialize weight with a small random value(like 0.0007)
If we take the small random value as a weight and bias like 0.0007 then Z will also get small and close to zero after differentiation on increasing the hidden layer.
And you will get a Vanishing Gradient Problem. It is extreme in the case of Tanh, and in the case of Sigmoid and Relu training will be slow.
4] Not to initialize weight with a large random value(0 to 1)
If we take the large random value as a weight and bias from 0 to 1 then Z will also get very large (i.e. more saturating value) after differentiation on increasing the hidden layer.
And you will get a Slow Convergence and the worst case will be a Vanishing Gradient Problem. It is extreme in the case of Tanh, and in the case of Sigmoid and Relu, it is a non-saturating function in a positive direction.
Xavier/Glorat and HE weight initialization
What can be done to avoid problems in weight initialization?
we need random weight as per the requirement in a good range or with a good variance which should not so less and not so large
- Xavier/Glorat Initialization
- He weight Initialization
Xavier Initialization, or Glorot Initialization - When working with Tanh or Sigmoid
It is an initialization scheme for neural networks. Biases are initialized be 0 and the weights Wij at each layer are initialized as:
\(W_{ij}\sim U[-\frac{1}{\sqrt n},\frac{1}{\sqrt n}]\)
The main idea behind Xavier Initialization is to set the initial values of the neural network's weights in such a way that they facilitate the training process and help prevent issues like vanishing or exploding gradients. Proper weight initialization is essential because it can significantly affect the convergence and performance of a neural network.
The Xavier Initialization method sets the initial weights for a given layer with a uniform or normal distribution based on the size of the layer's input and output. The specific formulas for Xavier Initialization differ between the uniform and normal distributions:
For a normal distribution:
The weight initialization formula for Xavier Initialization Normal distribution is np.random.randn(no. of input, no. of node) x \(\sqrt\frac{1}{n}\) OR \(\sqrt\frac{1}{fan-in}\)
Where U is a uniform distribution and n is the number of inputs coming to the nodes
If the value of no. of input(n) is greater then the weight will be lesser, If the value of no. of input(n) is lesser then the weight will be greater. This will help to keep normal distribution balanced
For a uniform distribution:
The weight initialization formula Xavier Initialization Uniform distribution in the range [-x, x] where x is \(\sqrt\frac{6}{fan-in + fan-out}\)
fan_in is the number of input units to the layer.
fan_out is the number of output units from the layer.
Xavier Weight Initialization Practical
Xavier Initialization aims to keep the weights in a range that balances the signal flowing forward and backward through the network. It helps in addressing the challenges of training deep neural networks by ensuring that the weights are initialized with suitable values, reducing the likelihood of vanishing or exploding gradients during backpropagation.
Keep in mind that Xavier Initialization is just one of several weight initialization techniques available, and the choice of initialization method may depend on the architecture and activation functions used in your neural network. It's often recommended to experiment with different initialization methods to find the one that works best for your specific task.
HE/ Kaiming initialization - When working with Relu
For a normal distribution:
It is an initialization method for neural networks that takes into account the non-linearity of activation functions, such as ReLU activations.
The weight initialization formula He Initialization Normal is np.random.randn(no. of input, no. of node) x \(\sqrt\frac{2}{n}\)OR\(\sqrt\frac{2}{fan-in}\)
n is the number of inputs coming to the nodes
For a uniform distribution:
The weight initialization formula He Initialization Uniform distribution in the range [-x, x] where x is \(\sqrt\frac{6}{fan-in}\)
fan_in is the number of input units to the layer.
fan_out is the number of output units from the layer.
For HE Normal Initializer-
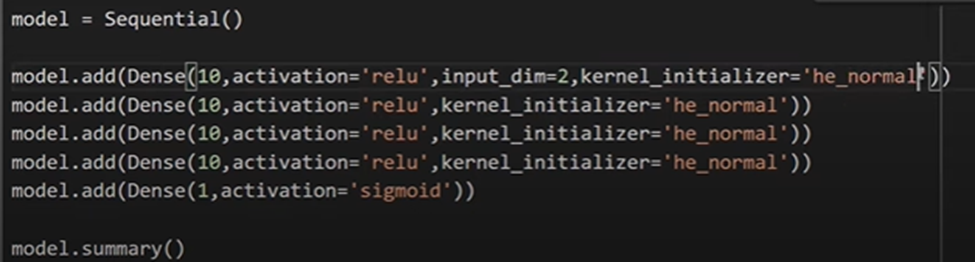
Four Kernel Initializer are he_normal, he_uniform, glorat_normal and glorat_uniform(default)