Deep Learning - ANN - Artificial Neural Network - Multilayer Perceptron (Notation & Memoization) Tutorial

MLP or Multilayer Perceptron Notation-

We have 4D data as there is 4 input X_i1, X_i2, X_i3, X_i4 in input layer

We have 3 nodes in hidden layer 1, So the total weight between input and hidden layer 1 is 4*3 = 12 weights and  3 bias

Similarly, between hidden layers 1 and 2, the total weight is 3*2 = 6 weight and 2 bias

Similarly, between hidden layer 2 and the Output layer, the total weight is 2*1 = 2 weight and 1 bias

Total Trainable Parameter = (12+3) + (6+2) + (2+1) = 15 + 8 + 3 = 26

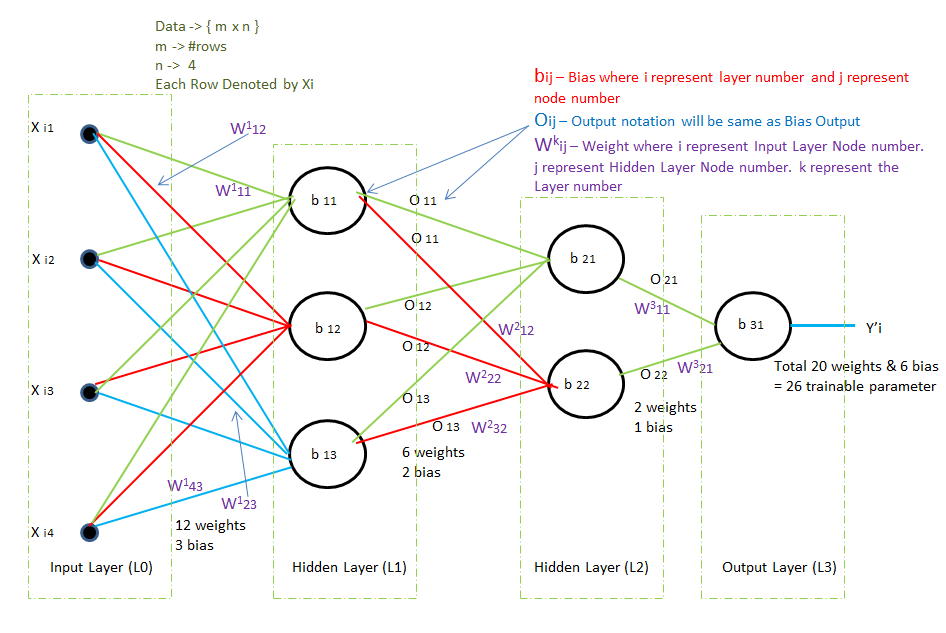
How to define bias?

b_ij = where i is layer number and j is node number.

b₁₁ will denote layer 1 (L1) with node 1

b₁₂ will denote layer 1 (L1) with node 2

b₂₁ will denote layer 2 (L2) with node 1

b₃₁ will denote layer 3(L3) with node 1

How to define Output?

The output will be the same as bias, e.g for bias b₁₁ the output will be O₁₁

How to define weight?

W^k_ij = Where k refers to which layer it is entering. i refer to from which node it is coming. j refers to which node it is entering of k^th layer.

W¹₁₁ = will denote it is going to layer 1. And coming from node 1, going to node 1

W¹₄₂ = will denote it is going to layer 1. And coming from node 4, going to node 2

W²₂₂ = will denote it is going to layer 1. And coming from node 2, going to node 2

W³₁₁ = will denote it is going to layer 3. And coming from node 1, going to node 1

Multi-Layer Perceptron

Multi-layer perception is also known as MLP. It is fully connected dense layers, which transform any input dimension to the desired dimension and it is capable of capturing non-linearity such as XOR.

A multi-layer perception is a neural network that has multiple hidden layers. To create a neural network we combine neurons together so that the outputs of some neurons are inputs of other neurons.

A multi-layer perceptron has one input layer and for each input, there is one neuron(or node), It has one output layer with a single node for each output and it can have any number of hidden layers and each hidden layer can have any number of nodes. A schematic diagram of a Multi-Layer Perceptron (MLP) is depicted below.

The activation function used here is the Sigmoid function instead of the Step Function. And loss function is Log Loss instead of Hinge Loss.

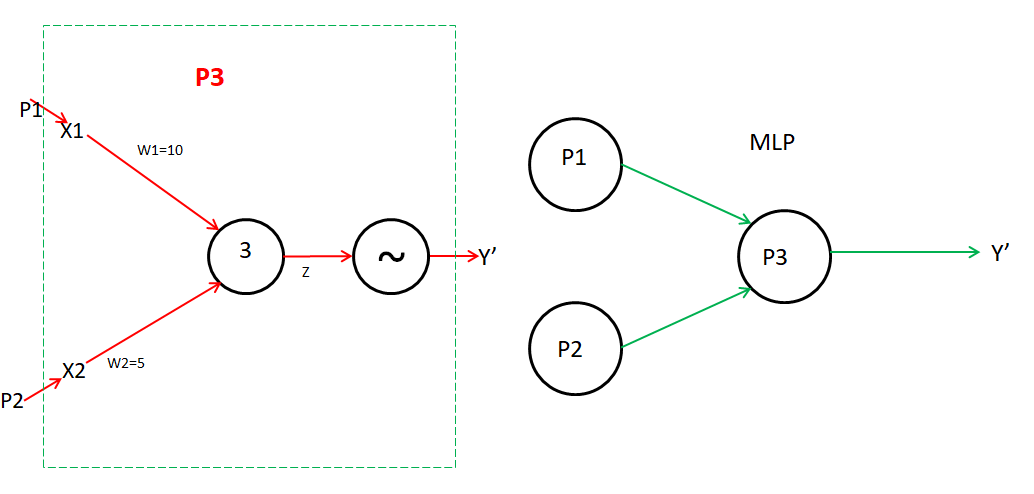
P3 is a perceptron, which gets the input from the output of another perceptron i.e. P1 and P2.

P3 input is x1 and x2. Where x1 is the output of P1 and x2 is the output of P2.

Hence, we are using a total of 3 Perceptrons. i.e. is known as multilayer perceptron

Here input layer is CGPA and IQ, the hidden layer is P1 and P2, and the output layer is P3.

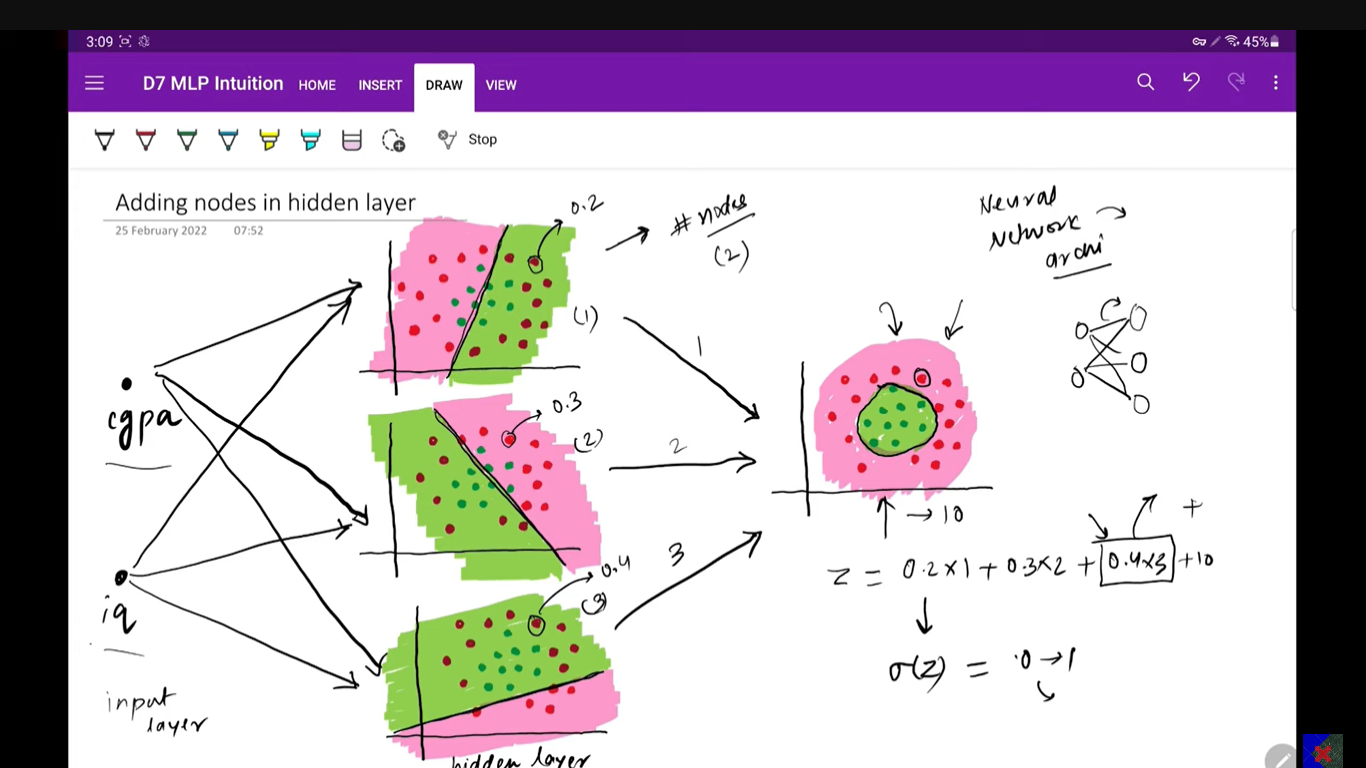
Adding nodes in the hidden layer will help you build more complex decision boundaries i.e. non linearity

OR

Adding more input nodes or Adding more output nodes (In case of a multiclass classification problem), will help you build a more complex decision boundary

OR

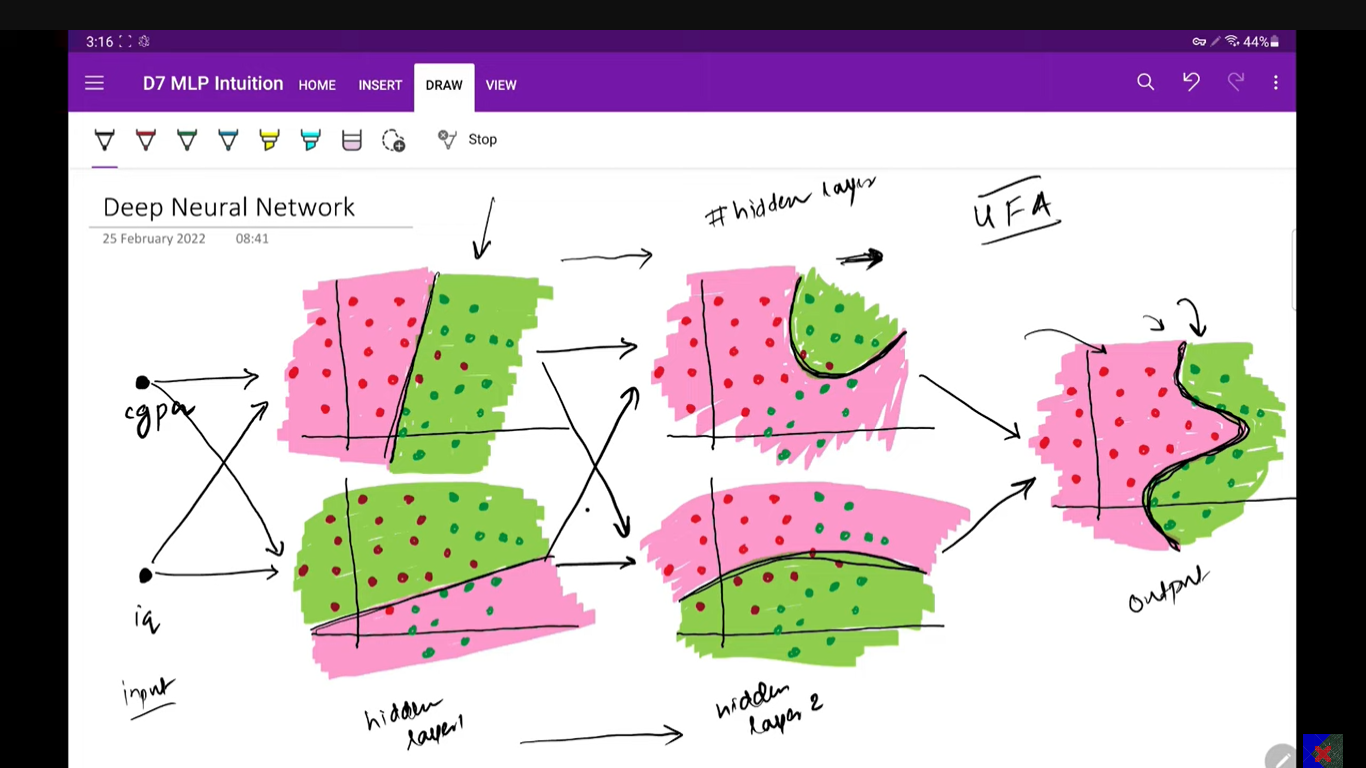
Adding more hidden layers i.e. making it a deep neural network, will also help you build a more complex decision boundary.

MLP or Multilayer Perceptron Memoization-

Memoization is an optimization technique that makes applications more efficient and hence faster. It does this by storing computation results in a cache and retrieving that same information from the cache the next time it's needed instead of computing it again.

MLP Memoization Fibonacci Practical

For finding the derivative of loss with respect to W¹₁₁ there are more than two paths, let's consider both path

i.e

1] W¹₁₁ -> O₁₁ ->O₂₁ -> Y’ -> L

2] W¹₁₁ -> O₁₁ ->O₂₂ -> Y’ -> L

So, finding the derivative of loss with respect to W¹₁₁ for both paths will be time consuming, i.e more calculations and this task will always repeated.

Hence, in this case, we will use memorization, in memorization it will store the value of each derivative, and will reuse it for other calculations. It will use more space, but it will take less time.

\(\frac{\delta L}{\delta W^1_{11}}=\frac{\delta L}{\delta Y'}[\frac{\delta Y'}{\delta O_{21}}\times\frac{\delta O_{21}}{\delta O_{11}}\times \frac{\delta O_{11}}{\delta W^1_{11}} +\frac{\delta Y'}{\delta O_{22}}\times\frac{\delta O_{22}}{\delta O_{11}}\times \frac{\delta O_{11}}{\delta W^1_{11}}]\)

Backpropagation --> Chain Difference (Rule) + Memoization

Hence backpropagation uses a combination of chain rule and memorization to make computation fast.