Deep Learning - ANN - Artificial Neural Network - Perceptron Loss Function Tutorial
Problem With Perceptron Trick-
1] Cannot quantify (we cannot define how good our model is?) -
If the point is misclassified, then the perceptron will make changes in the line(W1, W2, b).
If the point is not misclassified, then the perceptron will not make any changes in the line(W1, W2, b).
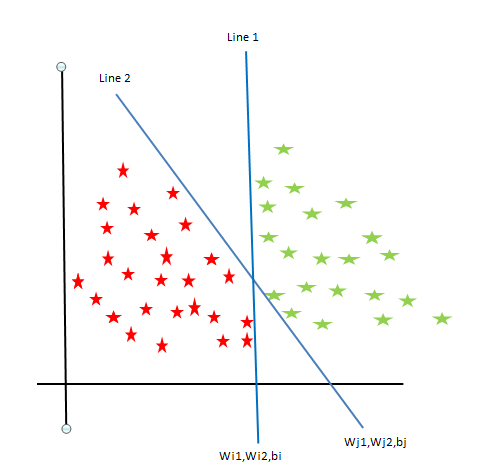
From the below image, both line 1 and line 2 classify the red and green areas. But, we cannot quantify the out of both line 1 and line 2 which one is the best line to classify
2] Might not fully converge
If the model will pick up the point on a random basis. then there might be a case where the model will pick up the same already classified point multiple times.
Due to this, the line will not get moved from the original position, and there is the possibility the line might not fully converge.
Perceptron Loss Function
The perceptron algorithm uses a loss function called the "hinge loss" function. Since the perceptron updates the weights in each iteration as follows: for all instance j, and for each weight i. Hence, weight tends to walk toward the error mitigation direction to reduce the loss to find the best line(weight and bias).
L(W1, W2, b) = \( \frac{1}{n}\sum_{i=1}^{n} 2(Y_i,f(X_i)) + \alpha R(W_1W_2)\)
\( \alpha R(W_1W_2)\) - Ignoring Regularization
L(W1, W2, b) = \(max(0, -Y_i f(X_i))\)
but \(f(X_i) = W_1X_1 + W_2X_2 + b\)
L = \( \frac{1}{n}\sum_{i=1}^{n} max(0,-Y_if(X_i))\)
n: #rows in data
Loss function depends on three things i.e. L(W1, W2, b)
we need to find such values of W1, W2, b. Due to this, the value of Loss becomes minimal. Therefore we will find argmin value of the Loss function.
L = \(argmin \frac{1}{n}\sum_{i=1}^{n} max(0,-Y_if(X_i))\)
Explanation Of Loss Function
L = \(\frac{1}{n}\sum_{i=1}^{n} max(0,-Y_if(X_i))\)
where f(Xi) = W1Xi1 + W2Xi2 + b
|
n row |
X1 |
X1 |
Y |
|
1 |
X11 |
X12 |
Y1 |
|
2 |
X21 |
X22 |
Y2 |
Xij -> where i is row and j is column
breaking down the loss function
let -Yif(Xi) = X
therefore max(0,-Yif(Xi)) = max(0, X)
if X>0 then the output will be X i.e
if X<0 then the output will be 0
Let's assume we have 2 points instead of n points.
L = \(\frac{1}{2}[max(0,-Y_1f(X_1)) + max(0,-Y_2f(X_2))]\)
for i=2.
Practical Example -
|
Student Placement Table |
|||||
|
CGPA |
IQ |
Placed - Yi - Actual Data |
Yi' - According to Model |
f(Xi) |
max(0,-Yif(Xi)) |
|
3 |
8 |
-1 |
1 |
+ve |
greater than 0 |
|
-3 |
1 |
-1 |
-1 |
-ve |
0 |
|
5 |
1 |
1 |
1 |
+ve |
0 |
|
-2 |
5 |
1 |
-1 |
-ve |
greater than 0 |
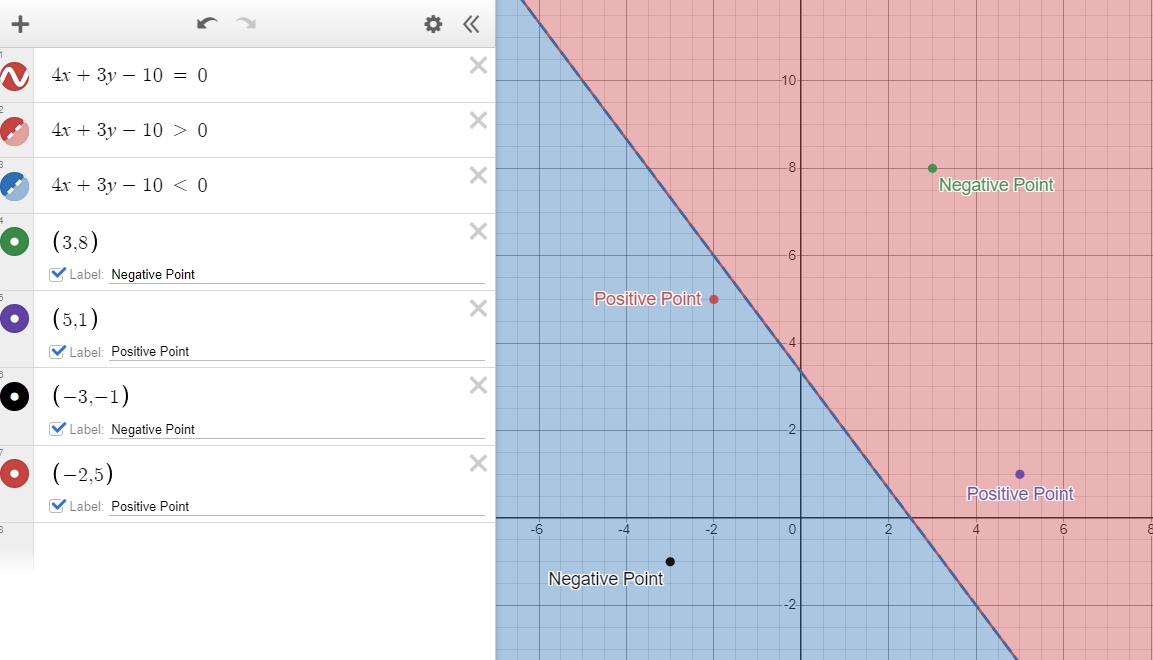
Value of f(Xi) for 2D i.e. f(X2) is W1X1 + W2X2 + b. therefore for points (3,8), it is on the positive side of the line. Hence W1X1 + W2X2 + b or f(X2) is positive.
Finding the value of W1, W2, and b. So that loss function will be the minimum
L = \(argmin \frac{1}{n}\sum_{i=1}^{n} max(0,-Y_if(X_i))\)
where f(Xi) = W1Xi1 + W2Xi2 + b
for i in epochs:
W1 = W1 + \(\eta \frac{\delta L}{\delta W_1}\)
W2 = W2 + \(\eta \frac{\delta L}{\delta W_2}\)
b = b + \(\eta \frac{\delta L}{\delta b}\)
To update the value we need to find 3 partial derivatives using the Gradient Descent
After this, we will differentiate loss function with respect to W1, W2, and b
\(\frac{\delta L}{\delta W_1} =\frac{\delta L} {\delta f(Xi)}\frac{\delta f(Xi)}{\delta W_1}\)
\(\frac{\delta L}{\delta W_1} = \begin{cases} 0 & \quad \text{if } Y_if(X_i)>=0\\ -Y_i & \quad \text{if } Y_if(X_i)<0\\ \end{cases} \)
\(\frac{\delta f(Xi)}{\delta W_1} = X_{i1}\)
\(\frac{\delta L}{\delta W_1} = \begin{cases} 0 & \quad \text{if } Y_if(X_i)>=0\\ -Y_iX_{i1} & \quad \text{if } Y_if(X_i)<0\\ \end{cases} \)
\(\frac{\delta L}{\delta W_2} = \begin{cases} 0 & \quad \text{if } Y_if(X_i)>=0\\ -Y_iX_{i2} & \quad \text{if } Y_if(X_i)<0\\ \end{cases} \)
\(\frac{\delta L}{\delta b} = \begin{cases} 0 & \quad \text{if } Y_if(X_i)>=0\\ -Y_i & \quad \text{if } Y_if(X_i)<0\\ \end{cases} \)
Practical Link - Perceptron Loss Function
Practically, Perceptron is equal to Logistic Regression, but technically they are the same if the activation function is sigmoid and the loss function binary cross entropy.
Perceptron OR Single Layer Perceptron – This is the simplest feedforward neural network and does not contain any hidden layer. It can learn only linear functions such as OR, AND
Multilayer Perceptron – A MultiLayer Perceptron has one or more hidden layers. It can learn both linear and non-linear functions such as XOR
Type Of Loss Function-
|
Loss Function |
Activation |
Output |
Activation Function Formula |
|
Hinge Loss |
Step function |
Perceptron – Binary Classification (-1 1) |
\(\mu = \begin{cases} 0 & \quad \text{if } x<0\\ 1 & \quad \text{if } x \geq 0 \end{cases} \ \) |
|
Log-Loss (binary cross entropy) |
Sigmoid |
Logistic Regression – Binary Classification (0 1) |
\(\sigma(z) = \frac{1}{1+ e^-z}\) |
|
Categorical Cross Entropy |
Softmax |
Softmax Regression, Probability – Multiclass classification |
\(\sigma(z) = \frac{e^{x_i}}{\sum_{j=1}^{K}{e^{x_j}}}\) |
|
Mean Squared Error |
Linear |
Linear Regression - Number |
Problem With Perceptron or Single Layer Perceptron-
Perceptron will work on only linear data(OR, AND), not on non-linear data(XOR)
Practical Link - Problem With Perceptron
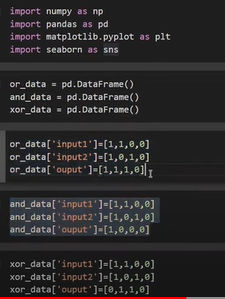
Created OR, AND, and XOR Dataframe

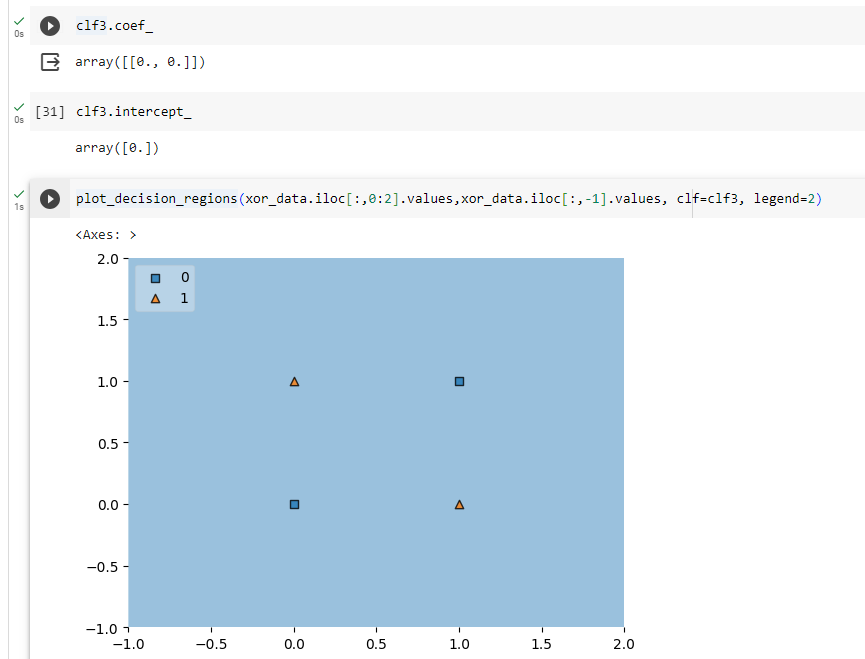
For AND data it has given clear-cut boundary

For OR data also it has given clear-cut boundary

But for XOR data it has given no clear-cut boundary