Deep Learning - RNN - Recurrent Neural Network - Backpropagation in RNN Tutorial

Taking the example of many-to-one RNN i.e Sentiment analysis

No. of the unique word - 5 i.e 'movie', 'was', 'good', 'bad', and 'not'

Converting it into vector-

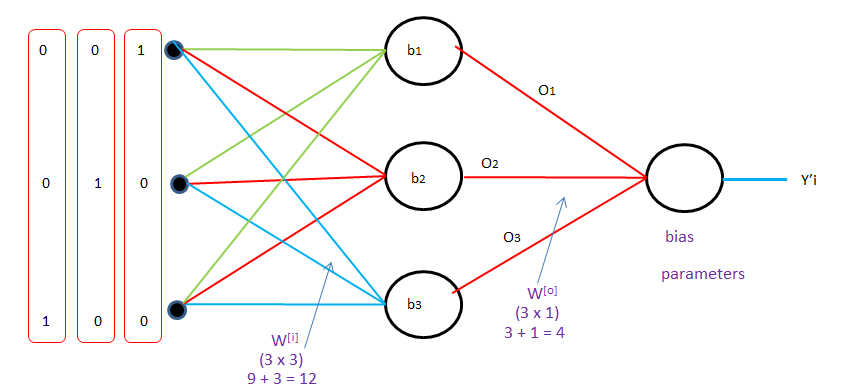
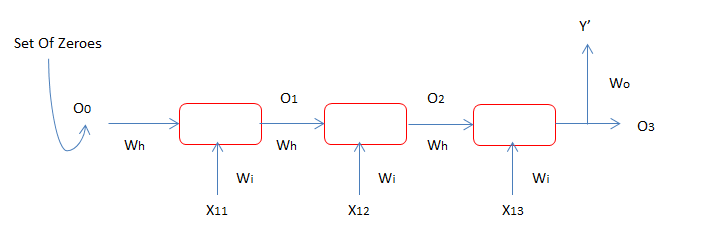
O₁ = f(X₁₁ W_i + O_oW_h )

O2 = f(X₁₂ W_i + O₁W_h )

O₃ = f(X₁₁ W_i + O₂W_h )

Y' = \(\sigma(O_3W_0)\)

L = -Y_i logY'_i - (1 - Y_i) log(1 - Y'_i)

After Loss Calculation, we need to minimize the loss using Gradient Descent.

for that, we need to find W_i, W_h, and W_o such values after which the L will be minimized.

 \(W_{i} = W_{i} - \eta\frac{\delta L}{\delta W_{i}}\)

\(W_{h} = W_{h} - \eta\frac{\delta L}{\delta W_{h}}\)

\(W_{o} = W_{o} - \eta\frac{\delta L}{\delta W_{o}}\)

\(\frac{\delta L}{\delta W_{0}} = \frac{\delta L}{\delta Y'} \frac{\delta Y'}{\delta W_{0}}\) 

\(\frac{\delta L}{\delta W_{i}} = \frac{\delta L}{\delta Y'} \frac{\delta Y'}{\delta O_{3}} \frac{\delta O_{3}}{\delta W_{i}} + \frac{\delta L}{\delta Y'} \frac{\delta Y'}{\delta O_{3}} \frac{\delta O_{3}}{\delta O_{2}}\frac{\delta O_{2}}{\delta W_{i}} + \frac{\delta L}{\delta Y'} \frac{\delta Y'}{\delta O_{3}} \frac{\delta O_{3}}{\delta O_{2}}\frac{\delta O_{2}}{\delta O_{1}}\frac{\delta O_{1}}{\delta W_{i}}\) 

summarizing the above for j=3

\(\frac{\delta L}{\delta W_{i}} = \displaystyle\sum_{j=1}^{3} \frac{\delta L}{\delta Y'} \frac{\delta Y'}{\delta O_{j}}\frac{\delta O_{j}}{\delta W_{i}}\) 

for j = 1, it will be \(\frac{\delta L}{\delta Y'} \frac{\delta Y'}{\delta O_{1}}\frac{\delta O_{1}}{\delta W_{i}} = \frac{\delta L}{\delta Y'} \frac{\delta Y'}{\delta O_{3}}\frac{\delta O_{3}}{\delta O_{2}}\frac{\delta O_{2}}{\delta O_{1}}\frac{\delta O_{1}}{\delta W_{i}}\)

for j = 2, it will be \(\frac{\delta L}{\delta Y'} \frac{\delta Y'}{\delta O_{2}}\frac{\delta O_{2}}{\delta W_{i}} = \frac{\delta L}{\delta Y'} \frac{\delta Y'}{\delta O_{3}}\frac{\delta O_{3}}{\delta O_{2}}\frac{\delta O_{2}}{\delta W_{i}}\)

for j = 3, it will be \(\frac{\delta L}{\delta Y'} \frac{\delta Y'}{\delta O_{3}}\frac{\delta O_{3}}{\delta W_{i}} = \frac{\delta L}{\delta Y'} \frac{\delta Y'}{\delta O_{3}}\frac{\delta O_{3}}{\delta W_{i}}\)

for j=n

\(\frac{\delta L}{\delta W_{i}} = \displaystyle\sum_{j=1}^{n} \frac{\delta L}{\delta Y'} \frac{\delta Y'}{\delta O_{j}}\frac{\delta O_{j}}{\delta W_{i}}\) 

\(\frac{\delta L}{\delta W_{h}} = \frac{\delta L}{\delta Y'} \frac{\delta Y'}{\delta O_{3}} \frac{\delta O_{3}}{\delta W_{h}} + \frac{\delta L}{\delta Y'} \frac{\delta Y'}{\delta O_{3}} \frac{\delta O_{3}}{\delta O_{2}}\frac{\delta O_{2}}{\delta W_{h}} + \frac{\delta L}{\delta Y'} \frac{\delta Y'}{\delta O_{3}} \frac{\delta O_{3}}{\delta O_{2}}\frac{\delta O_{2}}{\delta O_{1}}\frac{\delta O_{1}}{\delta W_{h}}\) 

similarly, we get  \(\frac{\delta L}{\delta W_{h}} = \displaystyle\sum_{j=1}^{n} \frac{\delta L}{\delta Y'} \frac{\delta Y'}{\delta O_{j}}\frac{\delta O_{j}}{\delta W_{h}}\)