Deep Learning - ANN - Artificial Neural Network - Activation Function Tutorial
What are the Activation Functions?
In artificial neural networks or ANN, each neuron forms a weighted sum of its inputs and passes the resulting scalar value through a function referred to as an activation function or step function
The activation function decides whether a neuron should be activated or not. The purpose of the activation function is to introduce non-linearity into the output of a neuron.
If a neuron has n inputs then the output or activation of a neuron is-
a = g(w1x1 + w2x2 + w3x3 + ….+ wnxn + b)
This function g is referred to as the activation function.
If the function g is taken as the linear function g(z) = z then the neuron performs linear regression or classification. In general, g is taken to be a nonlinear function to do nonlinear regression and solve classification problems that are not linearly separable. When g is taken to be a sigmoidal or 's' shaped function varying from 0 to 1 or -1 to 1, the output value of the neuron can be interpreted as a YES/NO answer or binary decision.
Why Activation Function is important?
Without an activation function, ANN will perform like a linear regression or logistic regression. If we use the Activation function(like relu), it will introduce non-linearity into the output of the neuron.
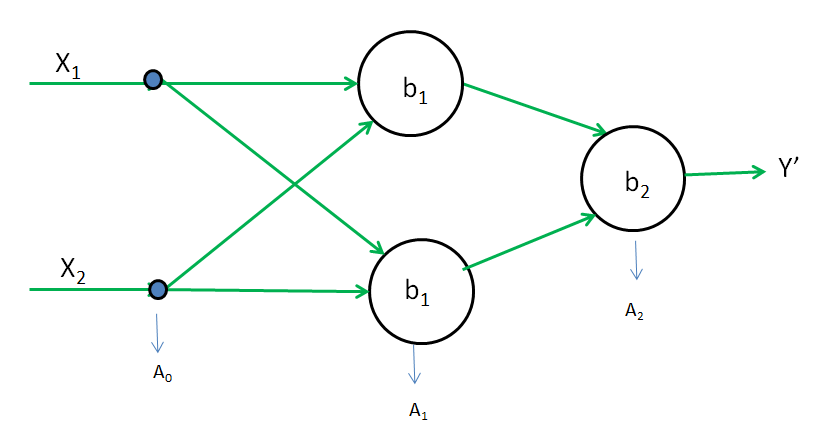
Z1 = W1A0 + b1
A1 = g(Z1) = Z1 ( g is linear function )
A2 = g(W2A1 + b1)
= W2A1 + b2 = W2(W1A0 + b1) + b2 = W2W1A0 + W2b1 + b2 = W'A0 + b'
A2 = Y' = W'A0 + b'
Input(A0) and Output(A2) have a difference of one-degree polynomial. which means the relationship is linear.
If g is not a linear activation function and it will be non linear activation function like sigmoid, relu, and tanh, then the output will be something complex
Ideal Activation Function-
- Activation functions should be such as sigmoid, relu, and tanh to capture non-linearity
- The activation function should be Differentiable, so we can apply gradient descent, and backpropagation on the model. (i.e relu)
- It should be computationally inexpensive i.e. simple, easy, and fast.
- Zero Centered – It should be normalized, so that it can converge fast. (i.e. tanh).
- Non-Saturating – the function which doesn’t get squeezed into a specific range i.e. relu range from max(0,x), sigmoid is a saturating function.
The function that gets squeezed into a specific range is saturating. For example - sigmoid range from 0 to 1, tanh range from -1 to 1. Saturating gradient descent will cause a vanishing gradient descent problem.
Type Of Activation Function-
Sigmoid Activation Function-
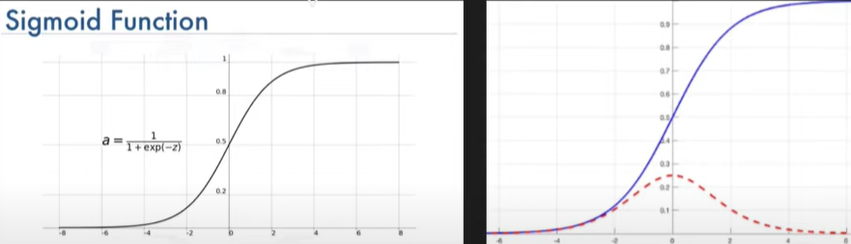
Formula-
\(f(x) = \frac{1}{1 +e^{-z}}\)
Advantages-
1] Its Output range from 0 and 1, will be treated as probability and used in an output layer. It is mostly used in binary classification problems (e.g probability greater than 0.5 is YES, less than is NO)
2] Non-linear used to capture non-linear pattern
3] Differentiable - used for gradient descent and backpropagation.
Disadvantages-
1] Saturated Function i.e. it ranges from 0 to 1, that causes vanishing gradient problem. As there is no update(no training) i.e. Wn = W0, that is why we never used sigmoid in the hidden layer. It is mostly used in the output layer in case of a binary classification problem.
2] Non-Zero Centered - It is not normalized which results in slow training.
3] Computationally expensive – because of the exponential in the formula
Tanh Activation Function(HyperBolic Tangent Function)-
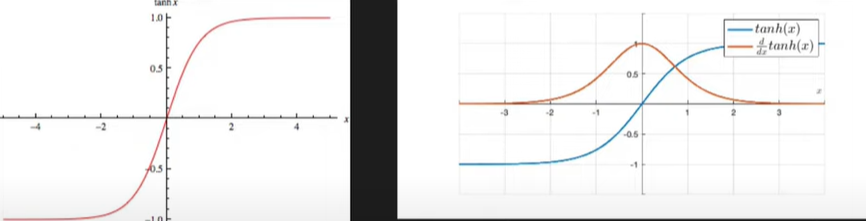
It ranges from -1 to +1
Formula-
\(f(x) = \frac{e^x - e^{-x}}{e^x +e^{-x}}\)
Derivative-
\(f(x) = (1 - tanh^2(x))\)
Advantages-
1] Non-Linear
2] Differentiable
3] Zero-Centered - It is normalized which results in fast training.
Disadvantages-
1] Saturated Function i.e it ranges from -1 to +1, causes a vanishing gradient problem
2] Computationally expensive – because of the exponential in the formula
Relu Activation Function-
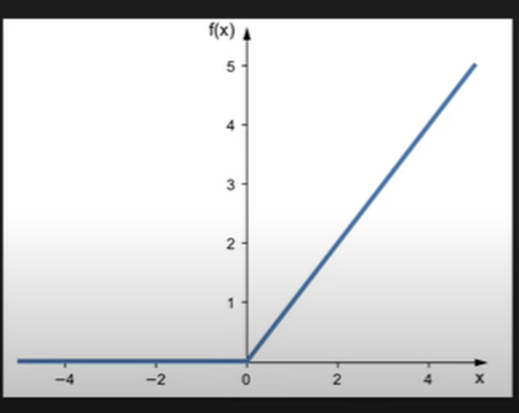
The Rectified Linear Unit or RELU is the most commonly used non-linear activation function in deep learning models. The function will return the value same as input directly if it is positive, otherwise, it will return zero, if it is negative.
Formula -
\(f(x) = max(0,x)\)
Range from 0 to x
Advantages-
1] Non-Linear
2] Not Saturated in the +ve region, because it range from 0 to x
3] Computationally inexpensive – not to calculate exponential, only x as given in the formula.
4] Converge – Faster as compared to sigmoid and tanh
Disadvantages-
1] Not completely differentiable.
2] Non–zero centered, but batch normalization can solve this problem.
In today date it is the best function, but still it has a dying RELU problem
Relu Variants – Leaky, Parametric, Elu, Selu
Dying Relu Problem-
The dying ReLU refers to the problem in which ReLU neurons become inactive and only provide output as 0 for any type of input.
It will become inactive forever. Such neurons will not play any role in discriminating the input and become useless in the neural network. If this process continues, over time you may end up with a large part of your network doing nothing. It will give low-level representation.
How dying relu problem occur?
If Z1(summation) becomes negative, then activation function a1 will also become zero, hence derivative of a1 with respect to z1 will also become zero.
Weight depends on the derivative of loss with respect to weight. But that derivative also depends on the derivative of a1 with respect to z1, which is already 0.
Hence, there will be no update in weight, which means the new weight and old weight are the same.
This is known as dying relu.
The dying relu problem occurs due to the negativeness of Z1 i.e. when Z1 = W1X1 + W2X2 + b1 will become negative.
i.e Z1 = W1X1 + W2X2 + b1 < 0
a1 = max(0, Z1) = 0
\(\frac{\delta a_1}{\delta z_1} = 0\)
\(W_{new_1} = W_{old_1} - \eta\frac{\delta L}{\delta W_1}\)
\(W_{new_2} = W_{old_2} - \eta\frac{\delta L}{\delta W_2}\)
because of dying relu \(\frac{\delta L}{\delta W_1} and \frac{\delta L}{\delta W_2} \)become 0 as it depends on \(\frac{\delta a_1}{\delta z_1} \)and \(W_{new} = W_{old}\)(there is no update)
The reason for the negative of Z1 is-
1. The learning rate is too high
2. There is a large negative bias.
1. The learning rate is too high
So, when you update the weight for the first time with a high learning rate, the weight will get negative. Due to this in the next cycle whole Z1 becomes negative, and the dying relu problem will start.
2. There is a large negative bias.
If there is a large negative bias, then Z1 can also become negative, which is the cause of the dying relu problem. Also during updating bias can also become negative in the next cycle.
Why it is called permanent dead?
Once Z1 becomes negative, it cannot recover. due to the update, it will again become negative and negative.
What are the solutions?
1] Set a low learning rate
2] Set bias value as +ve i.e 0.01
3] Don’t use relu instead use Relu Variant.
Type Of Relu Variants-
1] Linear – Leaky Relu, Parametric Relu
2] Non-Linear – Elu, Selu
1] Leaky Relu
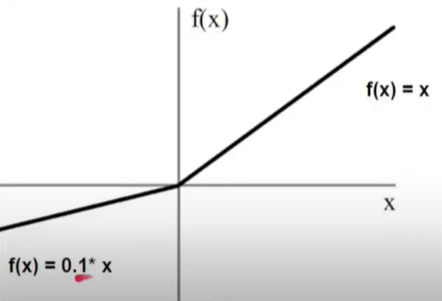
f'(Z) = max(0.01Z,Z)
Z>=0 → Z
Z<0 → \(\frac{1}{100}z\) (fraction of z) ⇒ -ve(Z) → not equal to 0 [0.01Z]
Derivative-
f'(Z)
Z>=0 → 1
Z<0 → 0.01
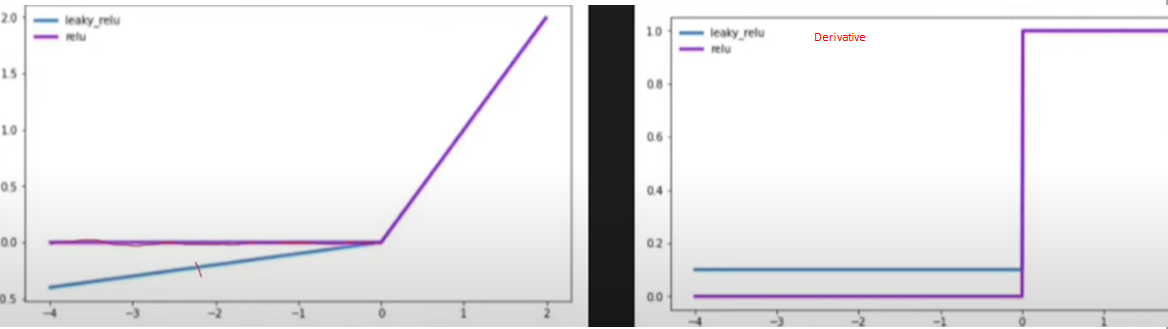
In leaky relu, a negative value of z will not become 0, it will become 0.01 of z. Hence derivative of –ve z value will be 0.01 and +ve will be the same as 1.
Due to this, during weight updation, the slope(derivative of loss with respect to weight) will not become 0.
2] Parametric Relu
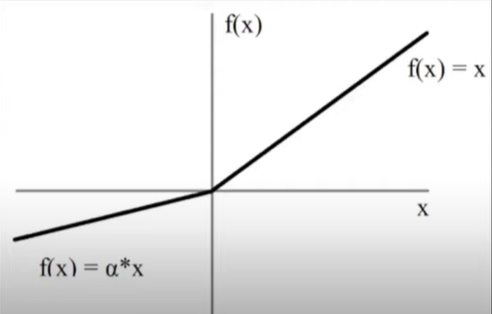
\(f(x) = \begin{cases} x & \quad \text{if } x \text{ > 0}\\ ax & \quad \text{otherwise} \end{cases} \)
a → trainable parameter
Exactly the same as leaky relu, the only difference is instead of 0.01 we use a flexible trainable parameter. a best value is found at the time of training according to given data.
The advantages are the same as leaky relu. No disadvantage
3] ELU – Exponentially Linear Unit
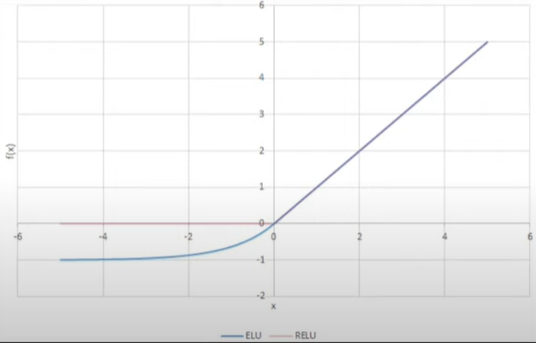
\(ELU(x) = \begin{cases} x & \quad \text{if } x \text{ > 0}\\ a(e^x - 1) & \quad \text{if } x \text{ < 0}\\ \end{cases} \)
Derivative Curve of ELU-
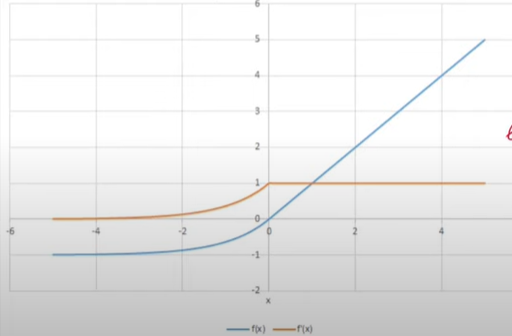
\(ELU'(x) = \begin{cases} x & \quad \text{if } x \text{ > 0}\\ ELU(x)+\alpha & \quad \text{if } x \text{ <= 0}\\ \end{cases} \)
Advantages-
1] Close to zero-centered, convergence toward the right solution is faster.
2] Will give better results on test data
3] No Dying Relu Problem
4] Always continuous as well as differentiable
Disadvantages-
1] Computation Expensive – because of exponential
4] SELU – Scaled Exponential Linear Unit
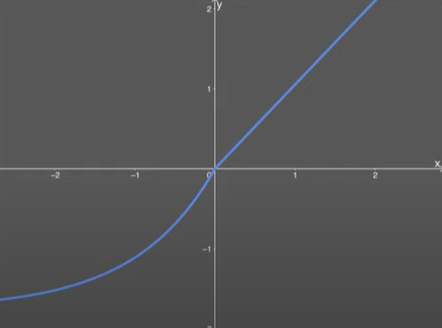
\(SELU(x) =\lambda \begin{cases} x & \quad \text{if } x \text{ > 0}\\ \alpha e^x - \alpha& \quad \text{if } x \text{ <= 0}\\ \end{cases} \)
\(\alpha\approx1.6732632423543772848170429916717 \)
\(\lambda\approx1.0507009873554804934193349852946\)
Derivative Curve Of SELU-
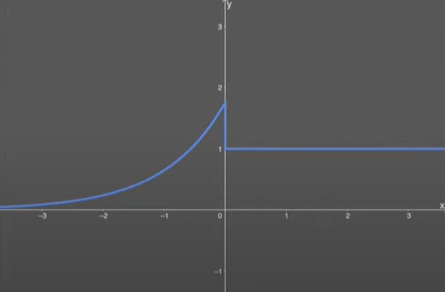
\(SELU(x) =\lambda \begin{cases} x & \quad \text{if } x \text{ > 0}\\ \alpha e^x & \quad \text{if } x \text{ <= 0}\\ \end{cases} \)
The advantage is the same as RELU
An extra advantage is it is self-normalizing (mean=0, standard deviation=1), therefore it converges faster.
Disadvantage - Not mostly used, because of less research