Statistics for AIML - Regression Metrics - Different Types Of Probability Distribution Tutorial
RANDOM VARIABLES – DISCRETE/CONTINUOUS
A variable that can take multiple values with different probabilities.
The mathematical function describing these possible values along with their associated probabilities is called Probability Distribution
Random Variable Type -
1] Discrete
2] Continuous
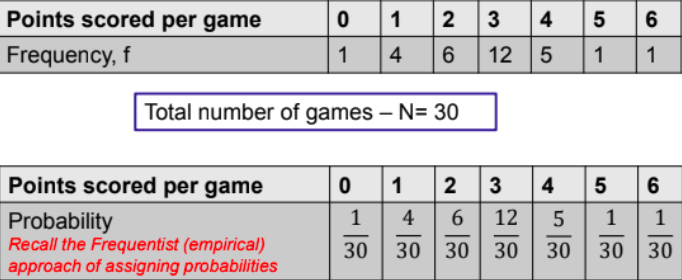
PROBABILITY MASS FUNCTION/PROBABILITY DENSITY FUNCTION
Ex - Sample Space Of Tossing 2 Coins is {HH, HT, TH, TT}
x = no. of heads in the toss of 2 coins
| x | 0 | 1 | 2 |
| P(x) | 1/4 | 1/2 | 1/4 |
Probability Mass Function
PMF(0) = 1/4
PMF(2) = 1/4
PMF(1) = 1/2
PMF(-1) = 0
Cumulative Distribution Function
The common Probability Distribution is as follows:
1. Bernoulli Distribution
2. Uniform Distribution
3. Binomial Distribution
4. Normal Distribution
5. Poisson Distribution
1. Bernoulli Distribution: A Bernoulli distribution has only two possible outcomes, namely 1 (success) and 0 (failure), and a single trial. So the random variable X which has a Bernoulli distribution can take value 1 with the probability of success, say p, and the value 0 with the probability of failure, say q or 1-p.
Example: whether it’s going to rain tomorrow or not where rain denotes success and no rain denotes failure and Winning (success) or losing (failure) the game.
2. Uniform Distribution: When you roll a fair die, the outcomes are 1 to 6. The probabilities of getting these outcomes are equally likely and that is the basis of a uniform distribution. Unlike the Bernoulli Distribution, all the n number of possible outcomes of a uniform distribution are equally likely.
Example: Rolling a fair dice.
3. Binomial Distribution: A distribution where only two outcomes are possible, such as success or failure, gain or loss, win or lose, and where the probability of success and failure is the same for all the trials is called a Binomial Distribution.
• Each trial is independent.
• There are only two possible outcomes in a trial- either a success or a failure.
• A total number of n identical trials are conducted.
• The probability of success and failure is the same for all trials. (Trials are identical.)
Example: Tossing a coin.
4. Normal Distribution: Normal distribution represents the behavior of most of the situations in the universe (That is why it’s called a “normal” distribution. I guess!). The large sum of (small) random variables often turns out to be normally distributed, contributing to its widespread application. Any distribution is known as a Normal distribution if it has the following characteristics:
• The mean, median, and mode of the distribution coincide.
• The curve of the distribution is bell-shaped and symmetrical about the line x=μ.
• The total area under the curve is 1.
• Exactly half of the values are to the left of the center and the other half to the right.
A normal distribution is highly different from Binomial Distribution. However, if the number of trials approaches infinity then the shapes will be quite similar.
5. Poisson Distribution: A distribution is called Poisson distribution when the following assumptions are valid:
• Any successful event should not influence the outcome of another successful event.
• The probability of success over a short interval must equal the probability of success over a longer interval.
• The probability of success in an interval approaches zero as the interval becomes smaller.
Example: The number of emergency calls recorded at a hospital in a day.
How To Calculate Sample Size Required?
You can use the margin of error (ME) formula to determine the desired sample size.
ME=t* Sn OR ME= t* n
• t/z = t/z score used to calculate the confidence interval
• ME = the desired margin of error
• S = sample standard deviation