Quantitative Aptitude - Quadratic Equation - Formula & Concept Tutorial

An equation of the form ax² + bx + c = 0, where a, b and c are real values and a ≠ 0, is called a quadratic equation in variable 'x'.

Here a, b, c are constants.

And x are the variable.

Let root of this quadratic equation is α and β

Therefore α + β =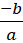    and αβ =

x =

1. If b² – 4ac = 0 or Discriminant D = 0 , then root are real and equal .
2. If b² – 4ac > 0 or Discriminant D > 0 , then root are real and unequal .
3. If b² – 4ac < 0 or Discriminant D < 0 , then root are imaginary and unequal .

For example –

• 5x² + 3x + 2 = 0

Using Normal method

Here a = 5, b = 3, c = 2

• • • 5x² + 5x – 2x + 2 = 0

    • 5x ( x - 1 ) – 2 ( x – 1 ) = 0

    • ( 5x – 2 ) ( x – 1 )

    • x = 2/5 , x = 1