Quantitative Aptitude - AP and GP - Formula & concept Tutorial

Arithmetic Progression

• An arithmetic progression is a sequence of numbers in which difference between any two consecutive number is result in common difference "d" . Here "a" is first number.
• The general form of an Arithmetic Progression is a, a + d, a + 2d, a + 3d and so on.
• For example Let a=3 and d=2. Then 3, 3 + 2, 3 + 2(2), 3 + 3(2),3 + 4(2), 3 + 5(2),………..….. Is 3 , 5 , 7 , 9 , 11 , 13……
•  “n” is no . of terms.
• To find last number (l) of AP . l= a + ( n – 1 )d
• Sum of first n terms of an AP:

S =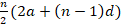 (when have first digit and common difference)

S = 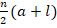   (when having first and last digit)

• T_n = S_n - S_n-1 , where T_n = n^th term
• When three quantities are in AP, the middle one is called as the arithmetic mean of the other two. If a, b and c are three terms in AP then b = (a+c)/2

For example  3 , 5 , 7 , 9 , 11 , 13…… are in AP with a=3 and d=2.

Here a=3,b=5,c=7 .therefore 5=(3+7)/2

Geometric Progression

• A geometric progression is a sequence in which each term is derived by multiplying the preceding term by a fixed number called the common ratio (r).
• The general form of a GP is a, ar, ar², ar³ and so on.
• Here a is first term.
• For example, let a= 2 and r=3 . then the sequence will be 2, 2(3) , 2(3²) , 2(3³),.... is 2, 6 , 18, 54, …….
• The nth term of a GP series is T_n = ar^n-1, where a = first term and r = common ratio =  .
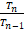• The formula applied to calculate sum of first n terms of a GP is S_{n =}  
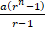
• When three quantities are in GP, the middle one is called as the geometric mean of the other two. If a, b and c are three quantities in GP and b is the geometric mean of a and c i.e. b =√ac
• The sum of infinite terms of a GP series S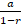_∞=  where 0< r<1.
• If a is the first term, r is the common ratio of a finite G.P. consisting of m terms, then the nth term from the end will be = ar^m-n.
• The nth term from the end of the G.P. with the last term l and common ratio r is l/(r^(n-1)) .

Harmonic Progression

• A series of terms is known as a HP series when their reciprocals are in Arithmetic Progression.
• The general form of a HP is 1/a, 1/(a+d), 1/(a+2d),…..
• And a, a + d, a + 2d are in Arithmetic Progression.
• The n^th term of a HP series is T_n =1/ [a + (n -1) d].
• To solve a problem on Harmonic Progression, one should make the corresponding AP series and then solve the problem.
• nth term of H.P. = 1/(nth term of corresponding A.P.)
• If three terms a, b, c are in HP, then b =2ac/(a+c).