Statistics for AIML - Regression Metrics - Different types of Sampling Tutorial

What is Sampling?

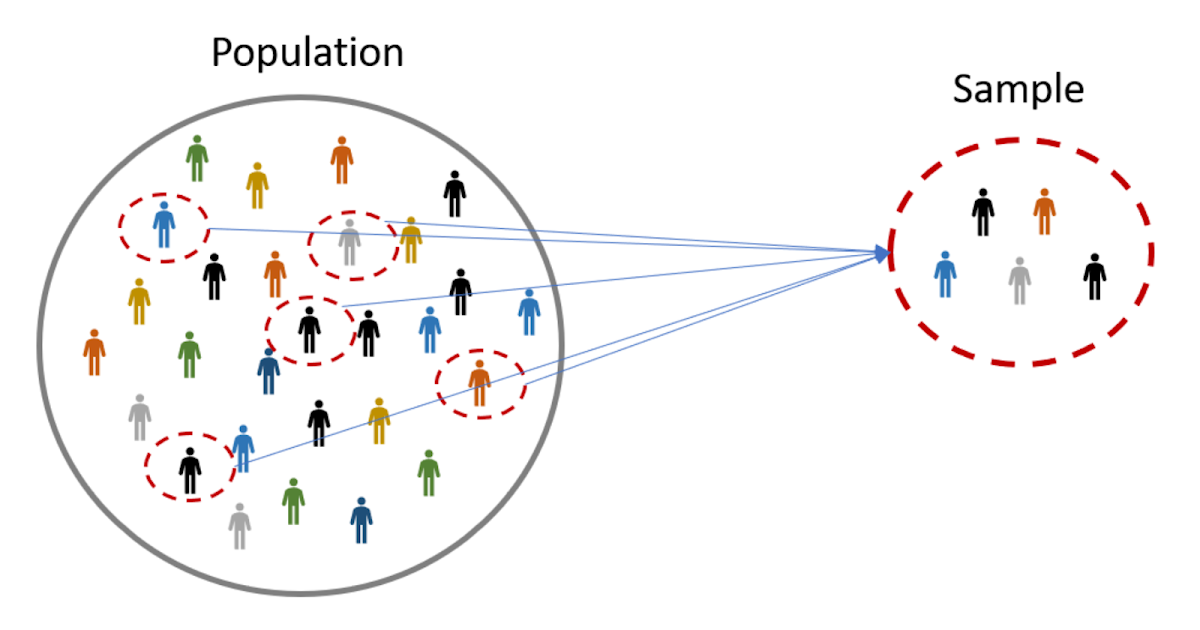
Sampling is a method that allows us to get information about the population based on the statistics from a subset of the population (sample), without having to investigate every individual.

NEED FOR SAMPLING

Why do we need Sampling?

• Sampling is done to draw conclusions about populations from samples, and it enables us to determine a population’s characteristics by directly observing only a portion (or sample) of the population.
• Selecting a sample requires less time than selecting every item in a population
• Sample selection is a cost-efficient method
• Analysis of the sample is less cumbersome and more practical than an analysis of the entire population

TYPES OF SAMPLING

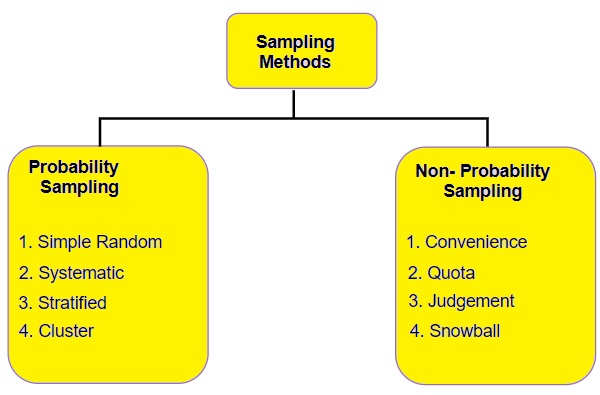
In probability sampling, every element of the population has the chance of being selected. Probability sampling gives us the best chance to create a sample that is truly representative of the population

In non-probability sampling, all elements do not have an equal chance of being selected. Consequently, there is a significant risk of ending up with a non-representative sample that does not produce generalizable results

Some of the Common Probability sampling ways are as follows:

• Simple random sample: One of the best probability sampling techniques that helps in saving time and resources, is the Simple Random Sampling method. Every member and set of members has an equal chance of being included in the sample randomly from the population. 

Example 1 - A teacher puts students' names in a hat and chooses without looking to get a sample of students.

Example 2 - In an organization of 500 employees, if the HR team decides on conducting team building activities, it is highly likely that they would prefer picking chits out of a bowl. In this case, each of the 500 employees has an equal opportunity of being selected.

Why it's good: Random samples are usually fairly representative since they don't favor certain members.

• Stratified random sample: The population is first split into groups. The overall sample consists of some members from every group. The members from each group are chosen randomly.

We use this type of sampling when we want representation from all the subgroups of the population. However, stratified sampling requires proper knowledge of the characteristics of the population.

Example—A student council surveys 100,100,100 students by getting random samples of 25,25,25 freshmen, 25,25,25 sophomores, 25,25,25 juniors, and 25,25,25 seniors.

Why it's good: A stratified sample guarantees that members from each group will be represented in the sample, so this sampling method is good when we want some members from every group.

• Cluster random sample: The population is first split into subgroups known as clusters. and a whole single cluster is randomly selected as a sample.

In the above example, we have divided our population into 5 clusters. Each cluster consists of 4 individuals and we have taken the 4th cluster in our sample. We can include more clusters as per our sample size.

This type of sampling is used when we focus on a region or area.

Why it's good: A cluster sample gets every member from some of the groups, so it's good when each group reflects the population as a whole.

• Systematic random sample: Members of the population are put in some order. A starting point is selected at random, and every nth member is selected to be in the sample.

• Rule: Say our population size is x and we have to select a sample size of n. Then, the next individual that we will select would be x/nth intervals away from the first individual. We can select the rest in the same way.
• For example, a researcher intends to collect a systematic sample of 500 people in a population of 5000. He/she numbers each element of the population from 1-5000 and will choose every 10th individual to be a part of the sample (Total population/ Sample Size = 5000/500 = 10).
• However, it might also lead to bias if there is an underlying pattern in which we are selecting items from the population. There should be no hidden pattern in the order.

Example - A principal takes an alphabetized list of student names and picks a random starting point. Every 20th student is selected to take a survey.

Some of the Common Non-Probability sampling ways are as follows:

• Convenience sampling: This is perhaps the easiest method of sampling because individuals are selected based on their availability and willingness to take part.

• Here, let’s say individuals numbered 4, 7, 12, 15, and 20 want to be part of our sample, and hence, we will include them in the sample.

• For example, start-ups and NGOs usually conduct convenience sampling at a mall to distribute leaflets of upcoming events or promotion of a cause – they do that by standing at the mall entrance and giving out pamphlets randomly.
• Convenience sampling is prone to significant bias, because the sample may not be the representation of the specific characteristics such as religion or, say the gender, of the population.

• Quota sampling:  In this type of sampling, we choose items based on predetermined characteristics of the population. 

For example, you could divide the population into strata and then select from each strata based on Quota. Consider that we have to select individuals having a number in multiples of four for our sample:

• Therefore, the individuals numbered 4, 8, 12, 16, and 20 are already reserved for our sample.
• In quota sampling, the chosen sample might not be the best representation of the characteristics of the population that weren’t considered.

• Snowball sampling:  In this technique, Existing people are asked to nominate further people known to them so that the sample increases in size like a rolling snowball. This method of sampling is effective when a sampling frame is difficult to identify.

• Here, we had randomly chosen person 1 for our sample, and then he/she recommended person 6, and person 6 recommended person 11, and so on.

                                                                             1->6->11->14->19

• There is a significant risk of selection bias in snowball sampling, as the referenced individuals will share common traits with the person who recommends them.

• Judgement sampling:  It is also known as selective sampling. It depends on the judgment of the experts when choosing whom to ask to participate.

Suppose, our experts believe that people numbered 1, 7, 10, 15, and 19 should be considered for our sample as they may help us to infer the population in a better way. As you can imagine, quota sampling is also prone to bias by the experts and may not necessarily be representative.