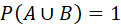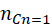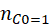Quantitative Aptitude - Permutation & Combination - Formula & Concept Tutorial

1. Factorial Notation:

Let n be a positive integer. Then, factorial n, denoted n! is defined as:

n! = n(n - 1)(n - 2) ... 3.2.1.

For example

1. 5! = ( 5 * 4 * 3 * 2 * 1 ) = 120
2. 1! = (1) = 1
3. 0! = 1

2. Permutations:

The different arrangements of a given number of things by taking some or all at a time, are called permutations.

Examples:

1. All permutations made with the letters a, b, c by taking two at a time are (ab, ba, ac, ca, bc, cb)

Here n ( total no. of letter ) = 3 , r ( taking two at a time ) = 2

This can be calculated using formula

No. of permutation of n things taken at a time.

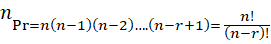
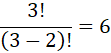
This 6 arrangement are (ab, ba, ac, ca, bc, cb)

2. All permutations made with the letters a, b, c taking all at a time are n!:
   ( abc, acb, bac, bca, cab, cba)

Here n and r both are same i.e 3

So by using formula

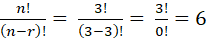
3. Combinations:

Each of the different groups or selections which can be formed by taking some or all of a number of objects is called a combination.

Examples:

Suppose we want to select two out of three boys A, B, C. Then, possible selections are AB, BC and CA.

Note: AB and BA represent the same selection (combination) but different permutation.

No. Of Combination -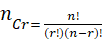

4. Number of permutation of n object =>
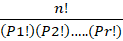
5. If A and B are exhaustive event then